On Embeddings for Numerical Features in Tabular Deep Learning

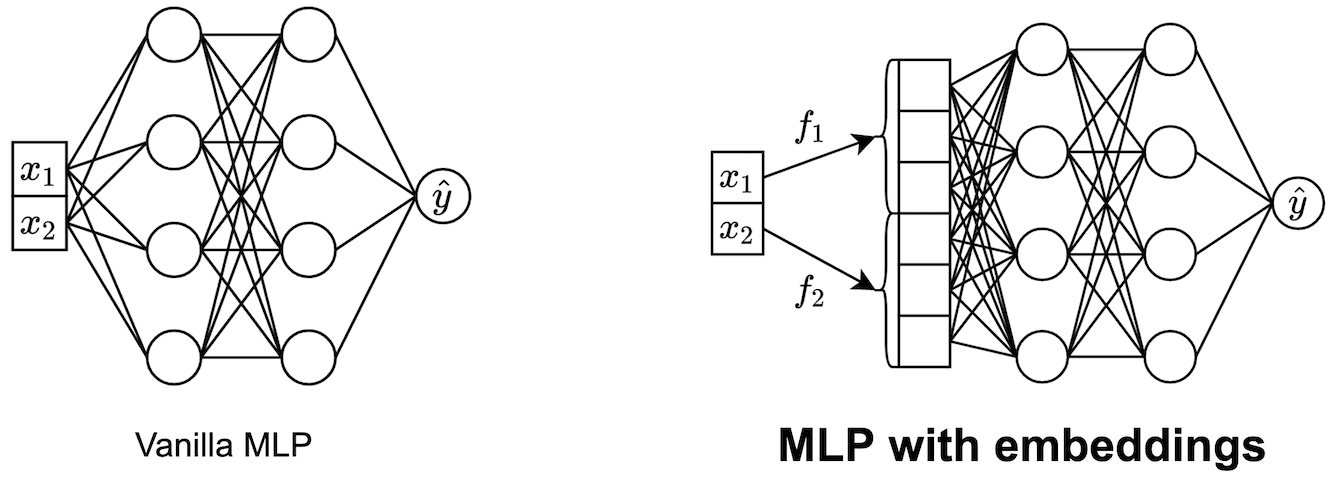
Recently, Transformer-like deep architectures have shown strong performance on tabular data problems. Unlike traditional models, e.g., MLP, these architectures map scalar values of numerical features to high-dimensional embeddings before mixing them in the main backbone. In this work, we argue that embeddings for numerical features are an underexplored degree of freedom in tabular DL, which allows constructing more powerful DL models and competing with gradient boosted decision trees (GBDT) on some GBDT-friendly benchmarks (that is, where GBDT outperforms conventional DL models). We start by describing two conceptually different approaches to building embedding modules: the first one is based on a piecewise linear encoding of scalar values, and the second one utilizes periodic activations. Then, we empirically demonstrate that these two approaches can lead to significant performance boosts compared to the embeddings based on conventional blocks such as linear layers and ReLU activations. Importantly, we also show that embedding numerical features is beneficial for many backbones, not only for Transformers. Specifically, after proper embeddings, simple MLP-like models can perform on par with the attention-based architectures. Overall, we highlight embeddings for numerical features as an important design aspect with good potential for further improvements in tabular DL.