Neural algorithmic reasoning with hint-based supervision
Neural algorithmic reasoning without intermediate supervision
Neural algorithmic reasoning focuses on building models that can execute classic algorithms. It allows one to combine the advantages of neural networks, such as handling raw and noisy input data, with theoretical guarantees and strong generalization of algorithms. Assuming we have a neural network capable of solving a classic algorithmic task, we can incorporate it into a more complex pipeline and train end-to-end. For instance, if we have a neural solver aligned to the shortest path problem, it can be used as a building block for a routing system that accounts for complex and dynamically changing traffic conditions. In our work [1], we study algorithmic reasoners trained only from input-output pairs, in contrast to current state-of-the-art approaches that utilize the trajectory of a given algorithm. We propose several architectural modifications and demonstrate how standard contrastive learning techniques can regularize intermediate computations of the models without appealing to any predefined algorithm’s trajectory.
Background The link has been copied to clipboard
The main challenge of neural algorithmic reasoning is the requirement of out-of-distribution (OOD) generalization. Since algorithms have theoretical guarantees to work correctly on any input from the domain of applicability, the actual difference between train and test data for neural algorithmic reasoners is potentially unlimited. Usually, the model is required to perform well on much larger input sizes compared to the instances used for training.
A significant step forward in developing neural algorithmic reasoners was made with the proposal of the CLRS Algorithmic Reasoning Benchmark [2]. This benchmark represents a set of several diverse algorithmic problems. CLRS proposes graphs as a general way to encode data since any particular algorithm can be expressed as manipulations over a set of objects and relations between them. For example, for sorting problems, we can treat every input list element as a separate node, and predict the output of the sorting stage with pointers between nodes representing the predecessor of a node in the sorted order.
The common way to tackle the OOD generalization problem is to use hints that represent intermediate steps of the algorithm’s execution. With hint-based supervision, the model is forced to imitate the exact trajectory of a given algorithm. Such supervision is considered a fundamental ingredient for progress in neural algorithmic reasoning.
Our approach The link has been copied to clipboard
In our paper [1], we argue that there are several disadvantages of using hints and investigate whether it is possible to train a competitive model using only input-output pairs.
First, we highlight some disadvantages of hint usage:
- Hints need to be carefully designed separately for each task and algorithm. Moreover, various model architectures may benefit from differently designed hints.
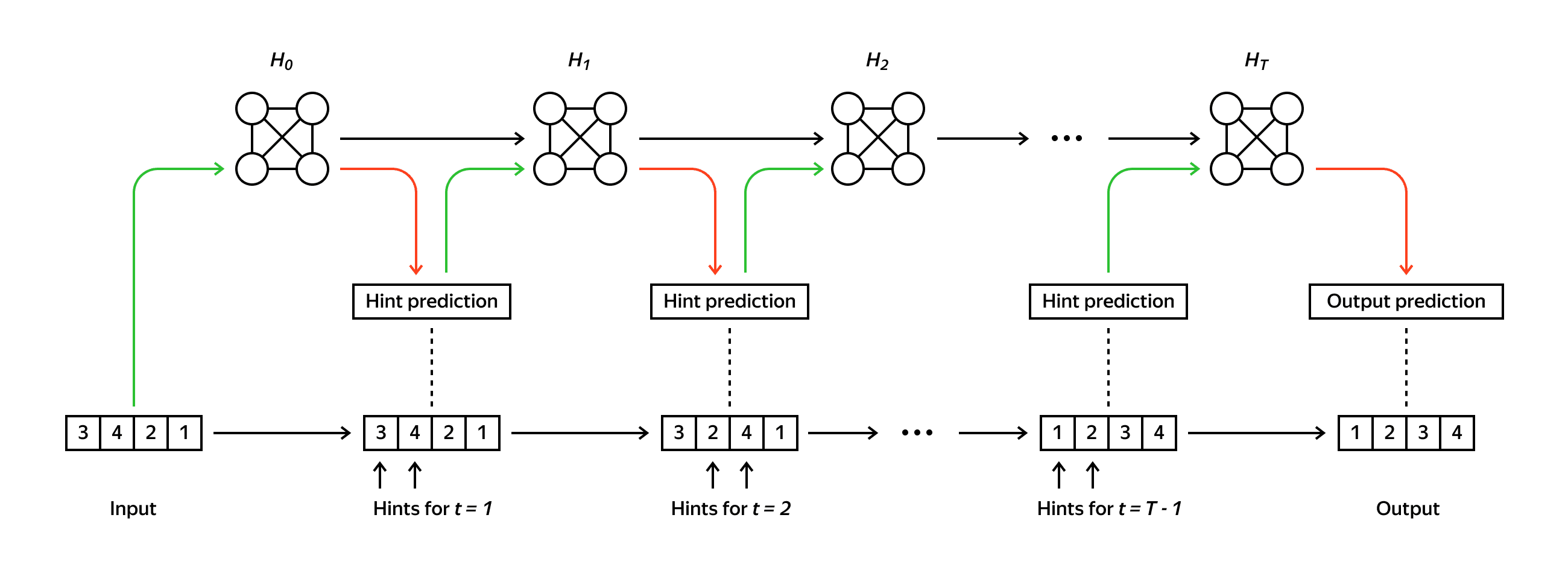
- Hints force the model to follow a particular trajectory. While this may help the interpretability and generalization of the trained model, following the algorithm’s steps can be suboptimal for a neural network architecture. For instance, it may force the model to learn sequential steps, while parallel processing can be preferable.
- A model trained with direct supervision on hints does not necessarily capture the dependencies between hints and the output of the algorithm. In other words, the model potentially can consider the hint sequence as a separate task (we refer to Section 3 of our paper).
- If a model is not restricted to a particular trajectory, it may potentially learn new ways to solve the problem, and thus by interpreting its computations, we may get new insights into the algorithms’ design.
To design our alternative approach, we make an observation that helps us to combine the advantages of learning algorithms only from input-output pairs with inductive bias improving the size generalization capabilities of the models.
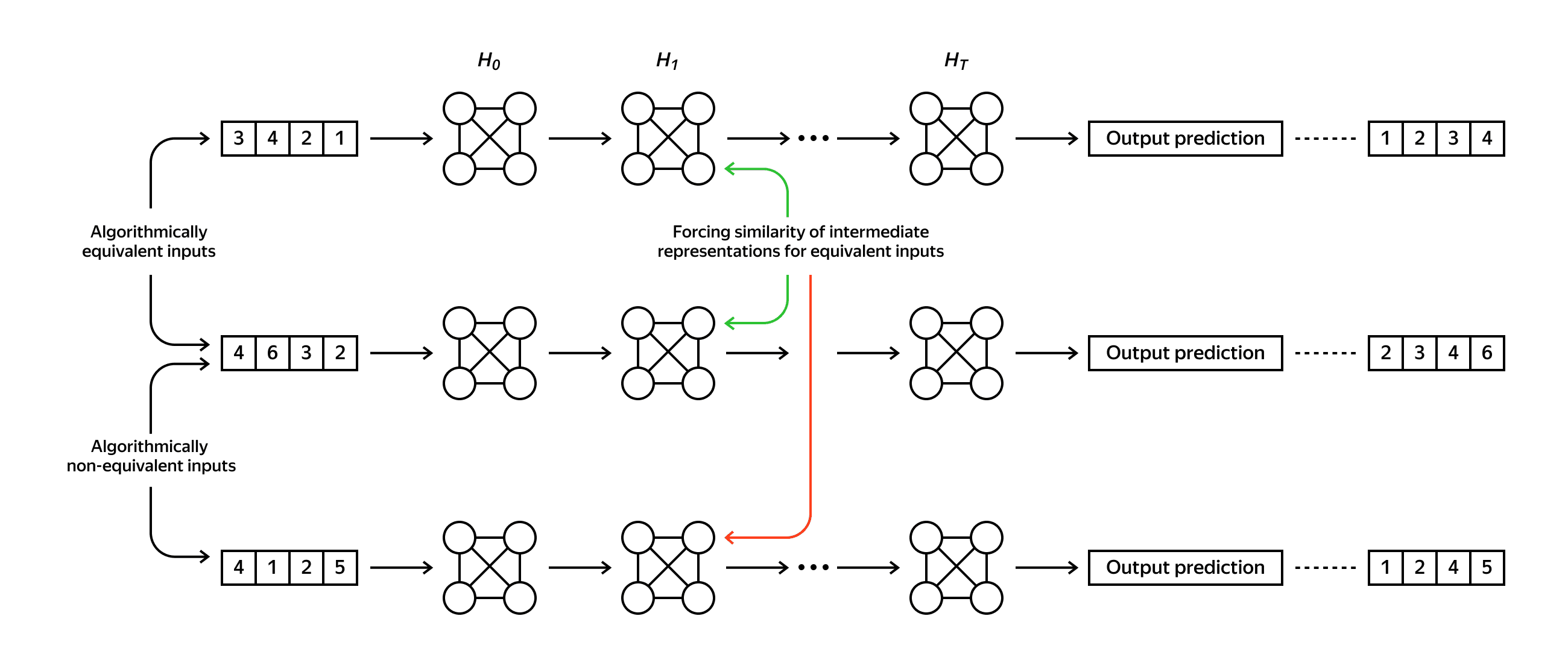
We note that the underlying combinatorial structure of some tasks allows us to describe the properties of the desired algorithm. Such properties can reduce the search space of the model while remaining in the wide range of possible algorithms, which can solve the given problem. For example, any comparison sort has the same trajectory for any pair of arrays with the same relative order of its elements. Given that, we can construct such a pair of different inputs that every step of any comparison sort algorithm is the same for both inputs. A less trivial example is the minimum spanning tree problem. A wide range of algorithms have the same execution trajectory on graphs with fixed topology (graph structure) and different weights on edges if the relative order of the corresponding edge weights is the same.
Forcing a model to act similarly on algorithmically equivalent inputs gives the model an additional signal about the problem without providing any constraints on computations that the model needs to follow. We can do it with classic contrastive learning techniques.
We also propose several architectural modifications for models trained without intermediate supervision that are aimed at making the comparison versus hint-based models more clear and fair. For example, we propose to reduce the difference between computational graphs of the models, which usually occurs in such comparisons. We refer to our paper for the details.
Results The link has been copied to clipboard
We compare our approach with several forms of hint usage. First, we consider the standard supervision of the hints, denoted as Baseline [3]. Then, No-hint is the model that completely ignores the hint sequence. Finally, Hint-ReLIC [4] utilizes an advanced way of using the hints. The last column demonstrates improvements obtained due to the proposed changes and self-supervised regularization. In particular, with this regularization, we achieve the best results for sorting (98.7%), significantly outperforming the existing models. We refer to the paper for additional details and experiments.
| Algorithm | No-hint | Baseline | Hint-ReLIC | No-hint (ours) |
| MST-Kruskal | 92.28 ± 0.82 | 91.18 ± 1.05 | 96.01 ± 0.45 | 93.15 ± 1.01 |
| MST-Prim | 85.33 ± 1.21 | 87.64 ± 1.79 | 87.97 ± 2.94 | 85.20 ± 1.77 |
| Insertion sort | 77.29 ± 7.42 | 75.28 ± 5.62 | 92.70 ± 1.29 | 98.74 ± 1.12 |
| Bubble sort | 81.32 ± 6.50 | 79.87 ± 6.85 | 92.94 ± 1.23 | 98.74 ± 1.12 |
| Quicksort | 71.60 ± 2.22 | 70.53 ± 11.59 | 93.30 ± 1.96 | 98.74 ± 1.12 |
| Heapsort | 68.50 ± 2.81 | 32.12 ± 5.20 | 95.16 ± 1.27 | 98.74 ± 1.12 |
| Binary Search | 93.21 ± 1.10 | 74.60 ± 3.61 | 89.68 ± 2.13 | 87.12 ± 2.23 |
| Minimum | 99.24 ± 0.21 | 97.78 ± 0.63 | 99.37 ± 0.20 | 99.99 ± 0.01 |
In summary, we propose several improvements to learning algorithms without intermediate supervision and demonstrate that the models without hints are competitive with hint-based models or even outperform them. We hope our work will encourage further investigation of neural algorithmic reasoners without intermediate supervision.
References
- G. Rodionov and L. Prokhorenkova. “Neural algorithmic reasoning without intermediate supervision”, NeurIPS 2023←
- P. Veličković, A. P. Badia, D. Budden, R. Pascanu, A. Banino, M. Dashevskiy, R. Hadsell, and C. Blundell. “The CLRS algorithmic reasoning benchmark”, ICML 2022←
- B. Ibarz, V. Kurin, G. Papamakarios, K. Nikiforou, M. Bennani, R. Csordás, A. J. Dudzik, M. Bošnjak, A. Vitvitskyi, Y. Rubanova, et al. “A generalist neural algorithmic learner”, LoG 2022←
- B. Bevilacqua, K. Nikiforou, B. Ibarz, I. Bica, M. Paganini, C. Blundell, J. Mitrovic, and P. Veličković. “Neural algorithmic reasoning with causal regularisation”, ICML 2023←