An illustration of the proposed separation between discrete and continuous data flows. Scalars can only affect the attention weights (Green) and can be modified with actions via ScalarUpdate (Blue).
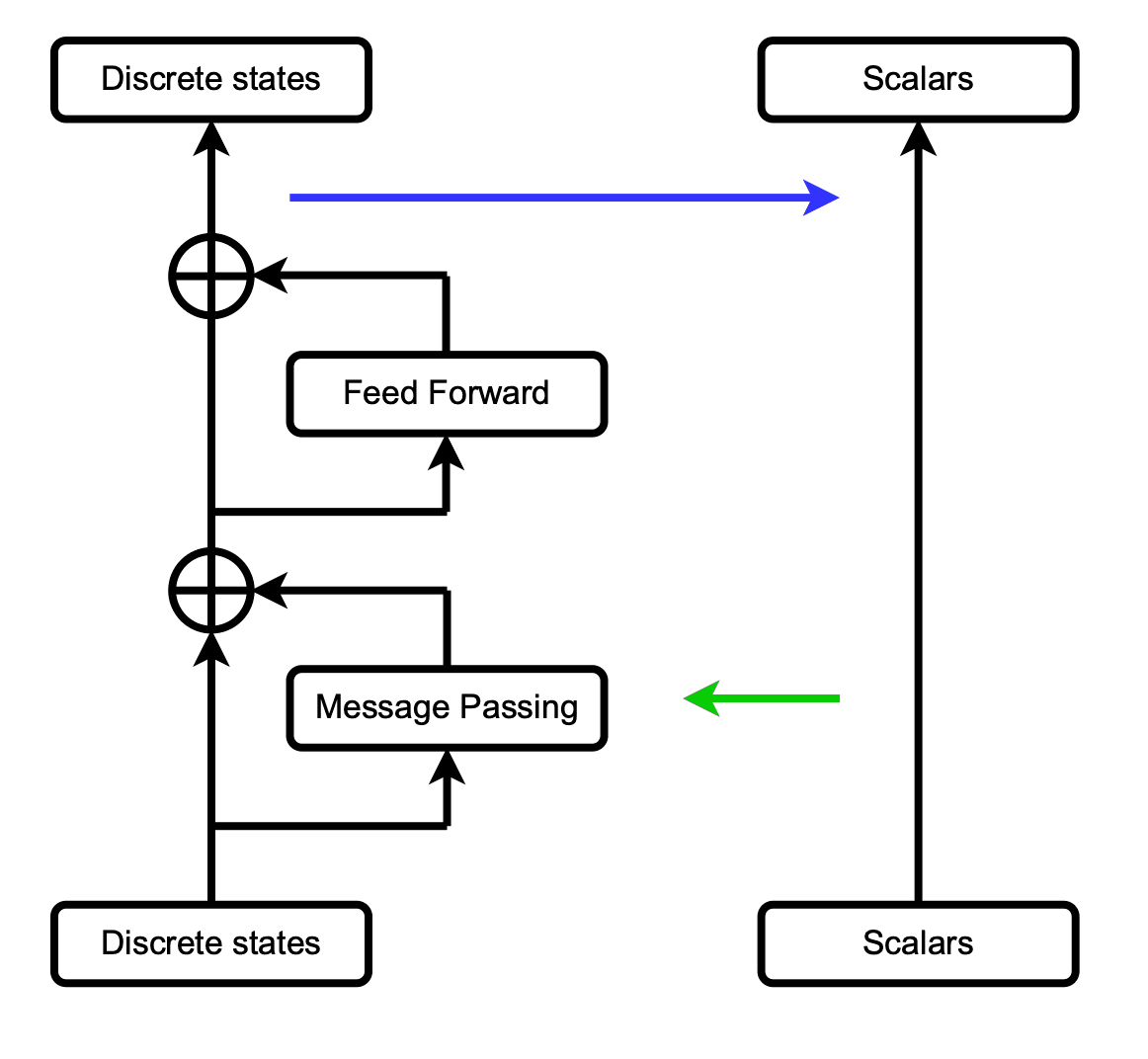
Discrete neural algorithmic reasoning
In this work, we achieve perfect neural execution of several algorithms by forcing the node and edge representations to be from a fixed finite set. Also, the proposed architectural choice allows us to prove the correctness of the learned algorithms for any test data.
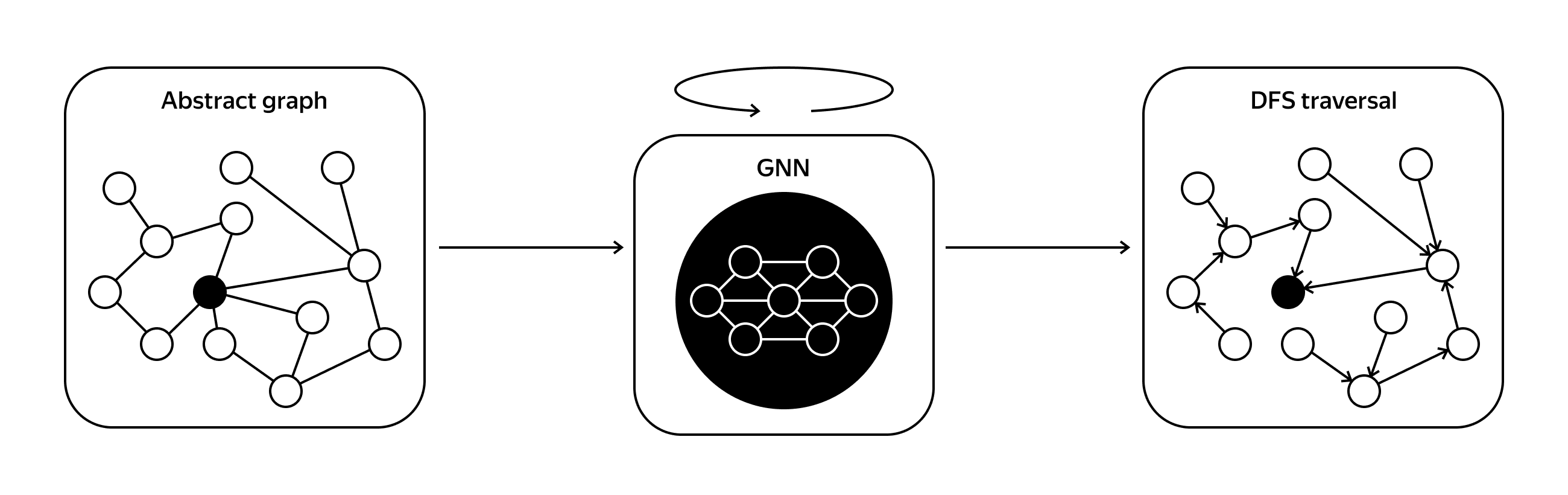
Neural algorithmic reasoning The link has been copied to clipboard
Learning to capture algorithmic dependencies in data and to perform algorithmic-like computations with neural networks are core problems in machine learning, studied for a long time using various approaches. Neural algorithmic reasoning aims to capture computations with neural networks via learning the models to imitate the execution of classical algorithms.
For the BFS problem, we are given a graph and a starting node. For each node, we predict its parent in the BFS tree.
Despite significant gains in the performance of neural reasoners in recent work, current models still struggle to generalize to the out-of-distribution (OOD) test data.
Usually, neural networks struggle to keep internal computations in the desired domain when encountering OOD data (e.g., larger neighborhood sizes in test data can cause significantly different node features, leading to wrong output predictions). In contrast, classical computation models (e.g., finite state machines) are defined as exact transitions between predefined states.
Outline of our work The link has been copied to clipboard
In our work [1], we propose to force neural reasoners to follow the execution trajectory as a combination of finite predefined states, which is important for both generalization ability and interpretability of neural reasoners. To achieve that, we start with an attention-based neural network and describe three building blocks to enhance its generalization abilities: feature discretization, hard attention and separating discrete and continuous data flows. In short, all these blocks are connected:
- State discretization does not allow the model to use complex and redundant dependencies in data;
- Hard attention is needed to ensure that attention weights will not be annealed for larger graphs. Also, hard attention limits the set of possible messages that each node can receive;
- Separating discrete and continuous flows is needed to ensure that state discretization does not lose information about continuous data.
Trained with supervision on the algorithm’s state transitions, such models can perfectly align with the original algorithm.
Our approach The link has been copied to clipboard
Performing algorithmic-like computations usually requires the execution of sequential steps, and the number of such steps depends on the input size. We use GNN as a recurrent unit for this purpose.
We start with Transformer convolution [2] and make several architecture modifications. The first one is enforcing the attention to be hard attention. Thus, for each attention head, each node receives the message only from one node. We found this property important for size generalization, as hard attention allows us to overcome the annealing of the attention weights for arbitrarily large graphs and strictly limits the set of messages that each vertex can receive.
After message computation, node and edge features are updated via MLP blocks depending on the current values and sent messages.
We also enforce all node and edge features to be from a fixed finite set, which we call states. We ensure such property by adding discrete bottlenecks after the message passing procedure.
For the BFS problem, we use two node states (Discovered, NotDiscovered) and two edge states (Pointer, NotAPointer). At the initial step, only the starting node has the state Discovered.
Clearly, most of the algorithmic problems operate with continuous or unbounded inputs (e.g., weights on edges). Usually, all input data is encoded into node and edge features, and the processor operates over the resulting vectors. The proposed discretization of such vectors would lead to the loss of information necessary for performing correct execution steps.
For the BFS problem, we use positional information to break ties in traversal order. Each node chooses as a parent the neighbor from the previous distance layer with the smallest index. As graphs can be arbitrarily large, operating with positional information would require infinite precision, so we propose not to discretize it.
Thus, we propose not to discretize continuous data and to use scalar inputs only in attention blocks as edge priorities $s_{ij}$. If scalars are related to the nodes, we assign them to edges depending on the scalar of the sender or receiver node.
We propose to use scalars simply by augmenting the key vectors $K_{ij}$ of each edge with the discrete indicator if the given edge has the “best” (min or max) scalar among the other edges to node $j$. Thus, scalars affect only the attention weights, not the messages and the node states.
This behavior is related to the theoretical primitive select best from RASP [3] and allows the attention block to attend depending on the predefined states and to use scalar priorities only to break ties.
For the BFS problem, the proposed selector allows us to exactly perform computations like “for unvisited node select the best visited neighbor”.
The proposed selector offers a read-only interface to scalar inputs (it is enough for problems like sorting, BFS and DFS), which is not expressive enough for most algorithms (e.g., the shortest paths problem). However, we note that the algorithms can be described as discrete manipulations over input data (e.g., addition instead of linear combination with arbitrary learnable weights), so we propose to learn discrete manipulations with scalars, which can be performed by external modules depending on discrete node/edge features (see the illustration below). We refer to our paper for the details.
Our architecture has two discrete bottlenecks: hard attention block and node/edge discretization after message passing. We optimize the corresponding discrete distributions using Gumbel reparametrization. During training, we anneal softmax temperatures to zeros. As the softmax temperature approaches zero, samples from the Gumbel-Softmax distribution become one-hot. At the inference, we replace the softmax operation with the argmax in both discrete bottlenecks.
Results The link has been copied to clipboard
We evaluate our approach on all problems from the SALSA-CLRS benchmark [4], namely BFS, DFS, Dijkstra, MST, MIS and Eccentricity. Trained with supervision on the algorithm’s state transitions, such models can perfectly align with the original algorithm, and we get perfect test scores for all tasks.
Also, as prior work [5][6] has shown the importance of jointly learning multiple algorithms, we test if the proposed discrete models are capable of multitask learning. Similarly to [5] and [6], which use task-dependent re-encoding of hints after each processor step, we use task-dependent discrete bottlenecks, keeping the processor the same for all tasks. We train a single processor network to execute all the algorithms (BFS, DFS, MIS, Prim, Dijkstra, Eccentricity) in a multitask manner. Our experiment shows that the proposed discrete reasoner is capable of multitask learning and demonstrates the perfect generalization scores in a multitask manner too.
Importantly, the proposed architectural choice allows us to prove the correctness of the learned algorithms for any test data: the key idea is that there is a finite number of node/edge states and due to the hard attention each node always receives the message from one node. All possible combinations can be directly evaluated. Thus, we can guarantee that for any graph size the model will mirror the desired algorithm, which is correct for any test size.
For the BFS problem, we can inspect the model and verify that the attention of Visited→Unvisited dominates the attention of Unvisited→Unvisited, so, at each step, each unvisited node will receive the message from a visited neighbor if such exists, or from an unvisited node otherwise. Then, by passing the corresponding states to the MLP after the message passing, we can check if the receiver node becomes visited or not regarding the received message, and so on.
Future work The link has been copied to clipboard
With the development of neural reasoners and their ability to execute classical algorithms on abstract data, it is becoming more important to investigate how such models can be applicable in real-world scenarios.
Also, while training neural reasoners without intermediate supervision is of interest for both a theoretical perspective and practical applications, training deep discretized models is known to be challenging. Thus, we leave a deeper investigation of learning interpretable neural reasoners without hints for future work.
References
- Rodionov G. and Prokhorenkova L. “Discrete neural algorithmic reasoning.” 2024.←
- Shi Y. et al. “Masked label prediction: Unified message passing model for semi-supervised classification.” 2020.←
- Weiss G., Goldberg Y., Yahav E. “Thinking like transformers.” ICML 2021.←
- Minder J, Grötschla F, Mathys J, Wattenhofer R. “SALSA-CLRS: A sparse and scalable benchmark for algorithmic reasoning.” LOG 2023.←
- Ibarz B. et al. “A generalist neural algorithmic learner.” LOG 2022.←
- Bohde M., Liu M., Saxton A., Ji S. “On the Markov property of neural algorithmic reasoning: Analyses and methods.” ICLR 2024.←