Structural distributional shifts for graph datasets

In reliable decision-making systems based on machine learning, models should comprise several important properties that allow users to rely on their predictions. One of them is robustness, the ability of a model to handle distributional shifts and provide high predictive performance even when the features of test inputs differ from those encountered during the training stage. If this property is hard to satisfy, a model should at least signal potential problems by providing some measure of uncertainty in its predictions. It then can be used to detect shifted samples and delegate the processing task to a human expert.

In node-level problems of graph learning, distributional shifts can be especially complex since samples are connected and depend on each other. It means that a distributional shift may occur not only in the features of nodes but also in the structure of an underlying network. In practice, these changes may happen simultaneously, creating a great challenge for Graph Neural Networks (GNNs) that use node features and graph structure to make predictions.

To evaluate the performance of graph models, it is essential to test them on diverse and meaningful distributional shifts. While some graph datasets may come with natural distributional shifts (e.g., based on timestamps)

[1], such shifts are rarely available. Most graph benchmarks that artificially create distributional shifts for node-level problems, such as the Graph OOD benchmark

[2], focus mainly on node features. At the same time, structural properties are also important for graph problems. The main issue in considering only the node features of graph datasets is that one has to perform screening over the available features to understand which can be used to split the data. Each new dataset requires a different approach and possibly special expert knowledge to create a node-level distributional shift. In contrast, the graph structure is the only common modality of different graph datasets that can be exploited similarly to model meaningful distributional shifts.

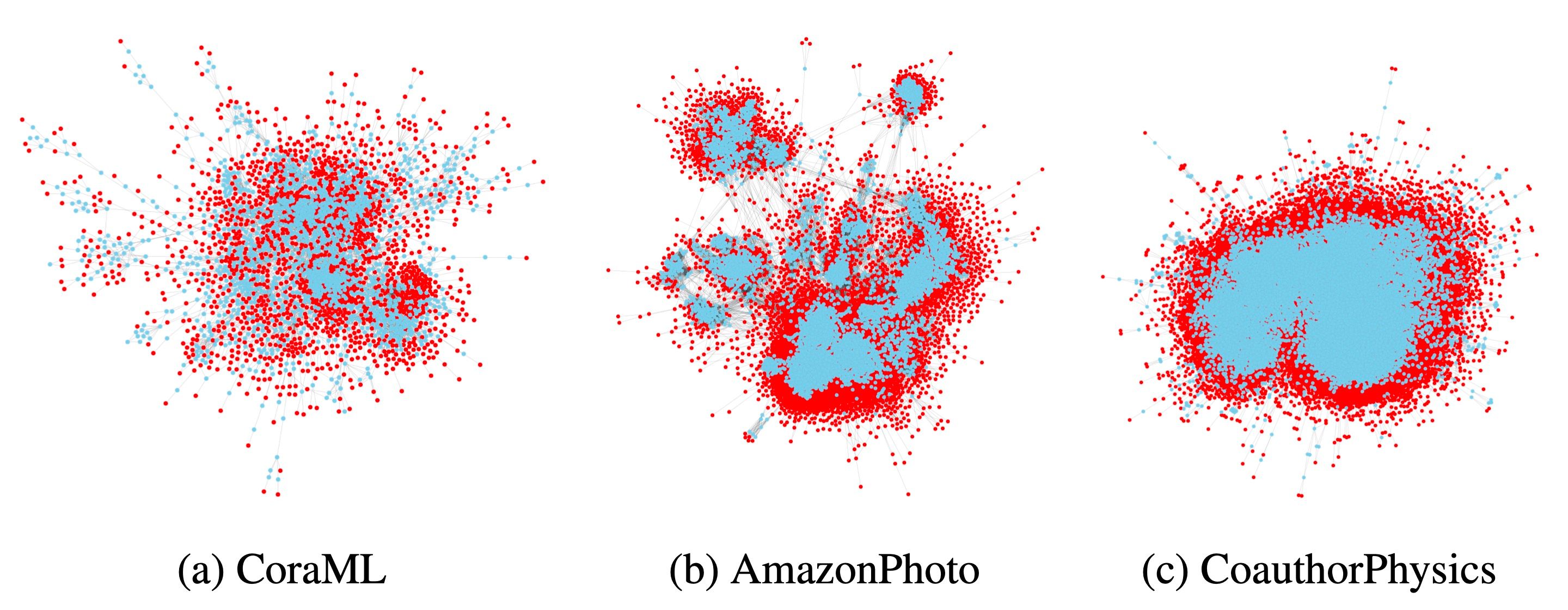
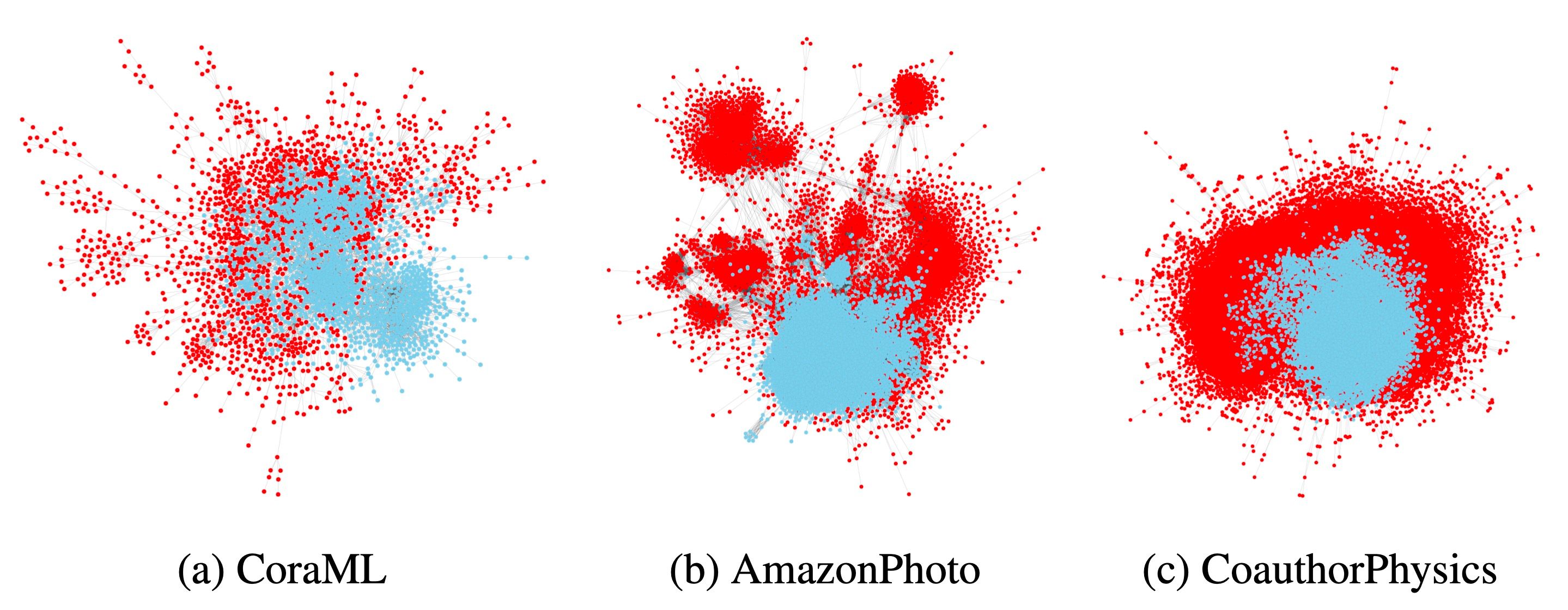
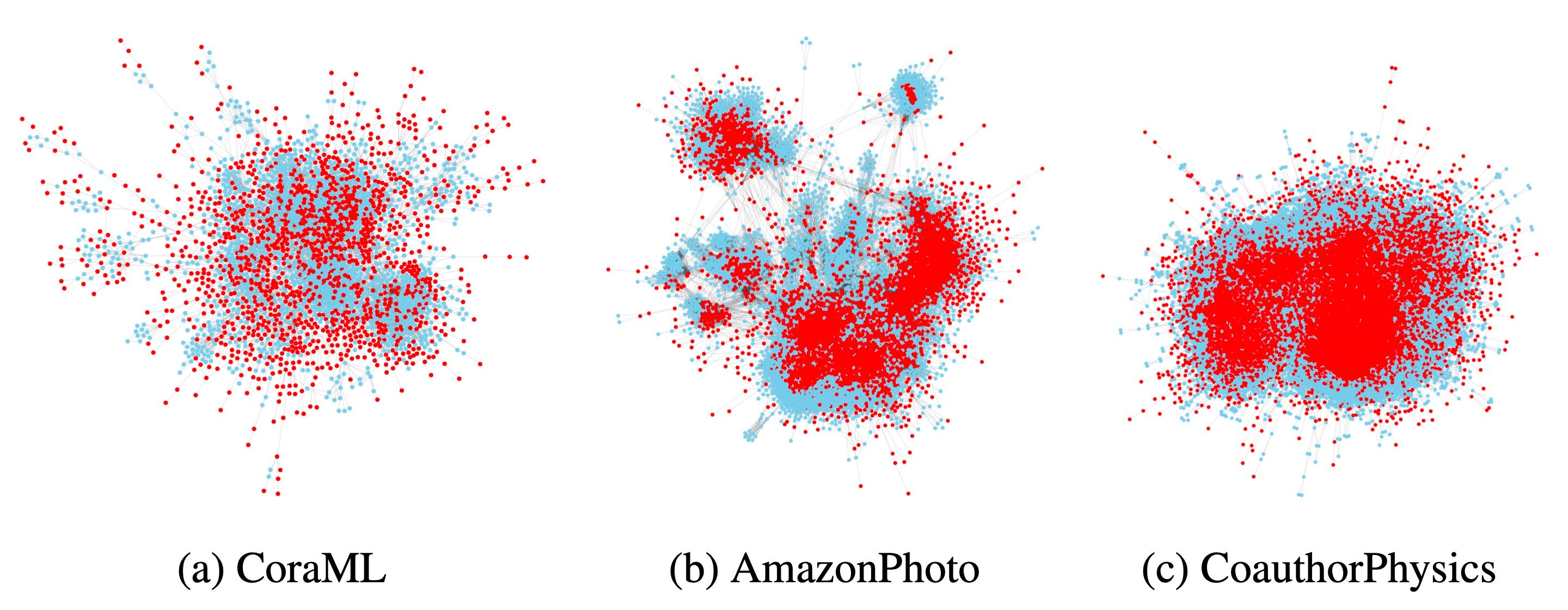
We propose

[3] a general approach for inducing diverse distributional shifts based on graph structure. In particular, we compute an arbitrary node-level characteristic that reflects some structural property of nodes. Then, we sort all nodes in ascending order of this characteristic and split them into different subsets — those with the smallest values are considered to be in-distribution (ID), while the remaining ones are out-of-distribution (OOD). As a result, we obtain a graph-based distributional shift where ID and OOD nodes have different structural properties.

Using this approach, we create data splits according to several structural node properties. In particular, our popularity-based shift models the situations when the training set consists of more popular (or important) items. This may happen if labels are assigned first to the most popular nodes that are considered to be particularly important for good prediction. However, when applying the model, making accurate predictions on less popular items is essential. Our popularity-based shift is based on PageRank, a well-known measure of node importance in a graph.

Popularity-based splits: the ID part (blue) consists of the core nodes, while the OOD subset (red) comprises the periphery.

Then, we consider a locality-based shift, which may happen when the data is labeled by exploring the graph starting from some node. In this case, the ID subset forms a local region in a graph, while the OOD nodes are from different graph regions. We model such a shift via Personalized PageRank (PPR) with restarts in the most popular node. Informally speaking, PPR measures how often a random walk starting from a given node visits other nodes, thus naturally capturing the locality notion.

Locality-based splits: the ID subset (blue) represents a local region around the most popular node, while the OOD part (red) contains more distant nodes.

Finally, we consider a density-based shift that separates dense and sparse regions of a graph. For this, we use local clustering coefficient, which measures the density within the one-hop neighborhood of a node.

Locality-based splits: the ID subset (blue) consists of more dense regions in a graph, while the OOD part (red) includes nodes with sparse neighborhood.

The proposed framework is quite flexible and allows one to easily extend it with other structural shifts or vary the fraction of nodes available for training and testing.

Our approach for creating data splits, along with three particular split strategies based on structural node properties proposed in our work, is implemented in the most widely used frameworks for machine learning on graphs: DGL and PyG. Via these links, one can find the examples of how to create structural distributional shifts for any graph dataset in just several lines of code.

Our experiments evaluate the proposed distributional shifts and show that they can be quite challenging for existing graph models. We also reveal that simple models often outperform more sophisticated methods on these challenging shifts. Finally, our experiments provide evidence of a trade-off between the quality of learned representations for the base classification task under structural distributional shift and the ability to separate the nodes from different distributions using these representations. For more details, please refer to our paper [3].

Structural distributional shifts for graph datasets

References