Papers accepted to NeurIPS 2023
Eight papers by the Yandex Research team (shown in bold below) and our collaborators have been accepted for publication at the Conference on Neural Information Processing Systems (NeurIPS 2023).
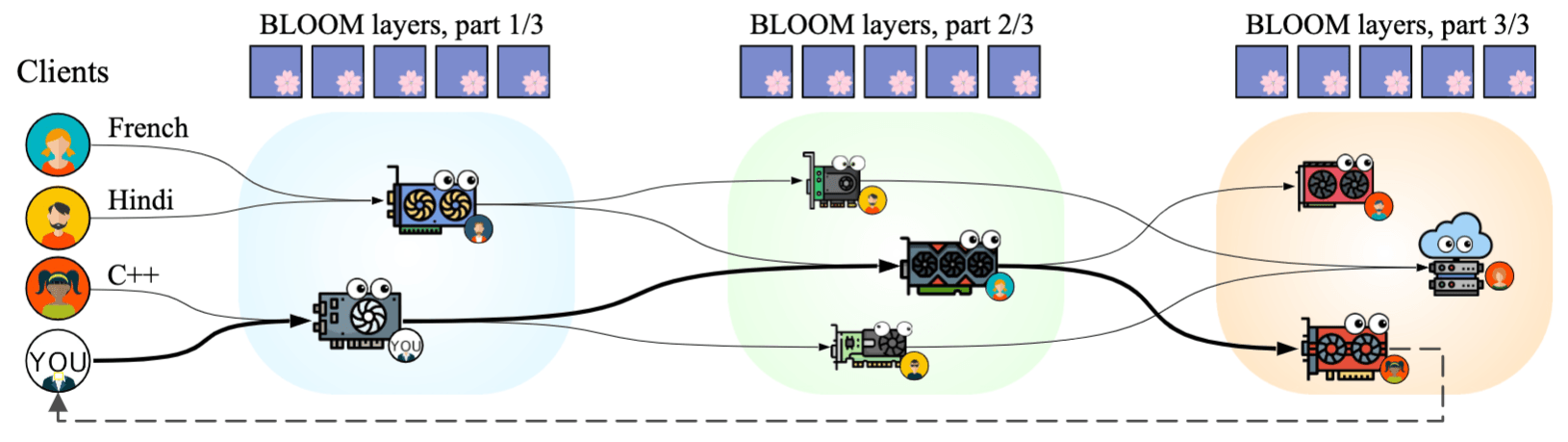
Distributed Inference and Fine-tuning of Large Language Models Over The Internet by Alexander Borzunov, Max Ryabinin, Artem Chumachenko, Dmitry Baranchuk, Tim Dettmers, Younes Belkada, Pavel Samygin, Colin Raffel

Large language models can be used to solve many NLP tasks and become even more capable with size. However, running 50B+ models efficiently requires high-end hardware, which is not accessible to researchers working outside large companies and research labs.
In this work, we investigate algorithms for cost-efficient inference and fine-tuning of LLMs, comparing local and distributed strategies. We show that large enough models can run efficiently over a geo-distributed network of consumer-grade GPUs connected over the Internet, even in the presence of network and hardware failures. This way, multiple research groups or volunteers can pool their hardware together and run such models significantly faster than if they ran the model independently. The algorithms proposed in this paper became the foundation of Petals — an open-source decentralized system for running LLMs.
Is This Loss Informative? Faster Text-to-Image Customization by Tracking Objective Dynamics by Anton Voronov, Mikhail Khoroshikh, Artem Babenko, Max Ryabinin
Diffusion models allow generating diverse and high-quality images even from the most complex prompts. However, to reproduce or customize an object from a real image, even the most detailed prompt will be of little help. The scientific community has proposed several methods for this task, such as Textual Inversion, DreamBooth, and Custom Diffusion, but their long runtime (up to 2 hours on a single GPU) is a huge drawback for practical applications.
In our work, we demonstrate that most of the optimization steps of these methods are unnecessary, but classic convergence indicators fail to show this. As a result, we propose a new objective that allows monitoring the learning process and making timely decisions about stopping.
Using this objective, we introduce an early stopping criterion named DVAR. Experiments on Stable Diffusion demonstrate that DVAR reduces training time by up to 8 times with no or minor losses in visual quality and identity preservation while preventing overfitting.
CAP: Correlation-Aware Pruning for Highly-Accurate Sparse Vision Models by Denis Kuznedelev, Eldar Kurtic, Elias Frantar, Dan Alistarh
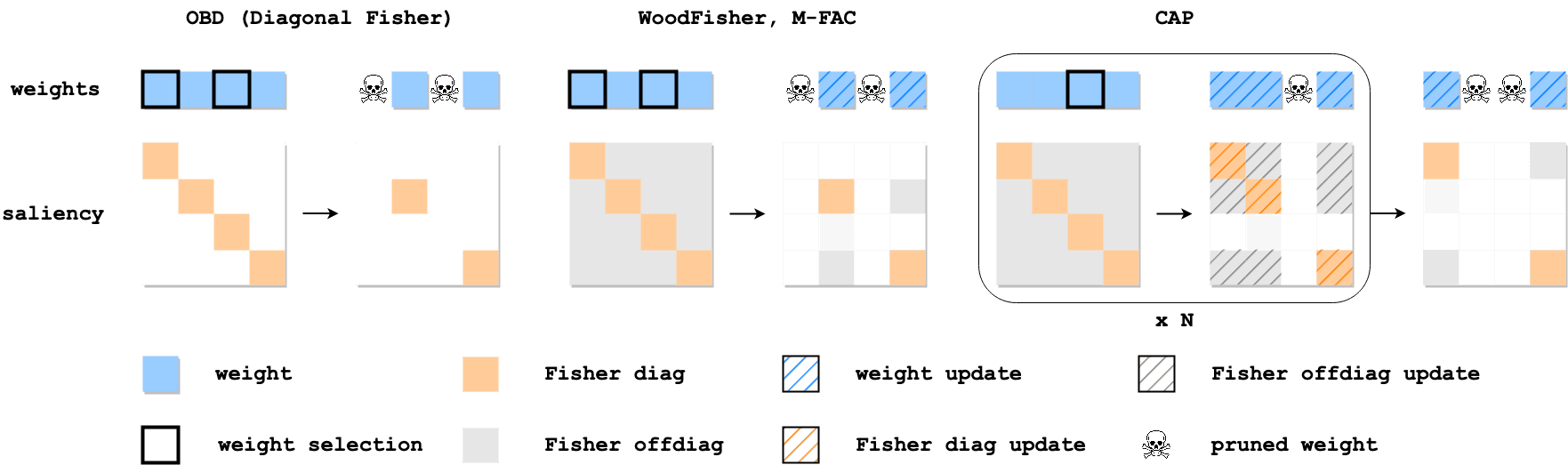
Driven by significant improvements in architectural design and training pipelines, computer vision has recently experienced dramatic progress in accuracy on classic benchmarks such as ImageNet. These highly accurate models are challenging to deploy, as they appear harder to compress using standard techniques such as pruning. We address this issue by introducing the Correlation Aware Pruner (CAP), a new unstructured pruning framework which significantly pushes the compressibility limits for state-of-the-art architectures. Our method is based on two technical advancements: a novel theoretically-justified pruner, leveraging accurate and efficient Hessian approximation, and a dedicated finetuning procedure for post-compression recovery. We validate our approach via extensive experiments on several modern vision models such as Vision Transformers (ViT), modern CNNs, and ViT-CNN hybrids, showing for the first time that these can be pruned to high sparsity levels with low impact on accuracy. Our approach is also compatible with structured pruning and quantization, and can lead to practical speedups of 1.5 to 2.4x without accuracy loss. To further showcase CAP's accuracy and scalability, we use it to show for the first time that extremely accurate large vision models, trained via self-supervised techniques, can also be pruned to moderate sparsities with negligible accuracy loss.
Characterizing Graph Datasets for Node Classification: Homophily-Heterophily Dichotomy and Beyond by Oleg Platonov, Denis Kuznedelev, Artem Babenko, Liudmila Prokhorenkova
Homophily is a graph property describing the tendency of edges to connect similar nodes; the opposite is called heterophily. It is often believed that heterophilous graphs are challenging for standard message-passing graph neural networks (GNNs), and much effort has been put into developing efficient methods for this setting. However, there is no universally agreed-upon measure of homophily in the literature. In this work, we show that commonly used homophily measures have some critical drawbacks. For this, we formalize desirable properties for a proper homophily measure and verify which measures satisfy which properties. Based on our results, we suggest using adjusted homophily as a more reliable homophily measure. Then, we go beyond the homophily-heterophily dichotomy and propose a new characteristic allowing one to further distinguish different sorts of heterophily. The proposed label informativeness (LI) characterizes how much information a neighbor's label provides about a node's label. We theoretically show that LI satisfies important desirable properties. We also observe empirically that LI better agrees with GNN performance compared to homophily measures, which confirms that it is a useful characteristic of the graph structure.
Evaluating Robustness and Uncertainty of Graph Models Under Structural Distributional Shifts by Gleb Bazhenov, Denis Kuznedelev, Andrey Malinin, Artem Babenko, Liudmila Prokhorenkova
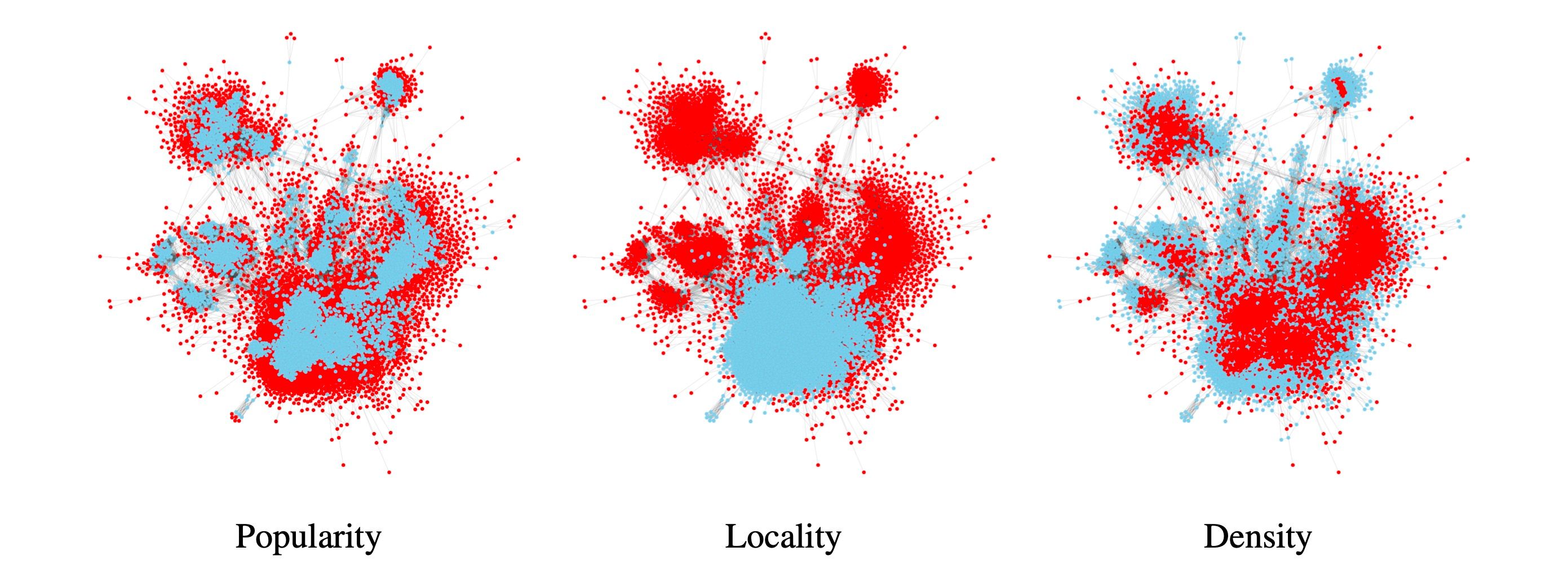
To evaluate robustness and uncertainty of graph models in node prediction problems, it is important to test them on diverse and meaningful distributional shifts. However, datasets with realistic shifts are rarely available. In our work, we propose a general approach for inducing diverse distributional shifts based on graph structure. Namely, we choose a particular node-level structural characteristic and split the nodes into in-distribution (ID) and out-of-distribution (OOD) subsets based on the values of this characteristic. As a result, we obtain a graph-based distributional shift where ID and OOD nodes have different structural properties. In our empirical study, we focus on three node characteristics: popularity, locality and density (they are visualized for one of the graph datasets in the picture below), and show that the corresponding distributional shifts can be very challenging for existing graph models, both in terms of their predictive performance and uncertainty estimation. We implement our approach in the two most widely used frameworks for machine learning on graphs: PyG and DGL. There, one may choose among the three aforementioned node characteristics or use custom structural properties to create data splits with distributional shifts. See our blog post for more details.
Neural Algorithmic Reasoning Without Intermediate Supervision by Gleb Rodionov, Liudmila Prokhorenkova
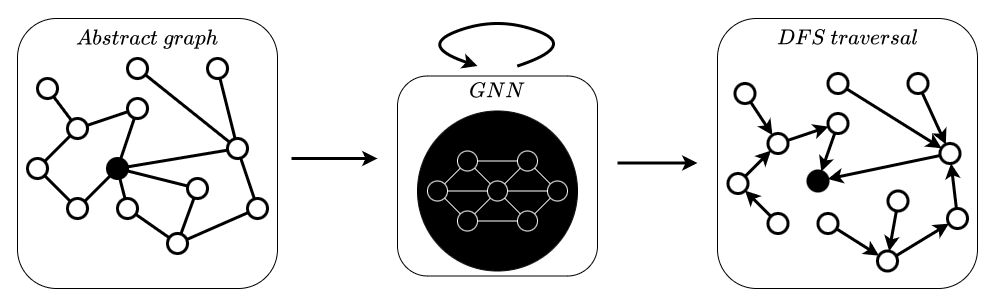
Neural Algorithmic Reasoning is an emerging area of machine learning focusing on building models which can imitate the execution of classic algorithms, such as sorting, shortest paths, etc. One of the main challenges is to learn algorithms that are able to generalize to out-of-distribution data, in particular with significantly larger input sizes. Recent work on this problem has demonstrated the advantages of learning algorithms step-by-step, giving models access to all intermediate steps of the original algorithm. In our work, we instead focus on learning neural algorithmic reasoning only from the input-output pairs without appealing to the intermediate supervision. We propose simple but effective architectural improvements and also build a self-supervised objective that can regularize intermediate computations of the model without access to the algorithm trajectory. We demonstrate that our approach is competitive to its trajectory-supervised counterpart on tasks from the CLRS Algorithmic Reasoning Benchmark and achieves new state-of-the-art results for several problems, including sorting, where we obtain significant improvements. Thus, learning without intermediate supervision is a promising direction for further research on neural reasoners.
Similarity, Compression and Local Steps: Three Pillars of Efficient Communications for Distributed Variational Inequalities by Aleksandr Beznosikov, Martin Takác, Alexander Gasnikov
Variational inequalities are a broad and flexible class of problems, including minimization, saddle point, and fixed point problems as special cases. Therefore, variational inequalities are used in various applications ranging from equilibrium search to adversarial learning. With the increasing size of data and models, today's instances demand parallel and distributed computing for real-world machine learning problems, most of which can be represented as variational inequalities. Meanwhile, most distributed approaches have a significant bottleneck - the cost of communications. The three main techniques to reduce the total number of communication rounds and the cost of one such round are the similarity of local functions, compression of transmitted information, and local updates.
In this paper, we combine all these approaches. Such a triple synergy did not exist before for variational inequalities and saddle problems, nor even for minimization problems. The methods presented in this paper have the best theoretical guarantees of communication complexity and are significantly ahead of other methods for distributed variational inequalities. Adversarial learning experiments on synthetic and real datasets confirm the theoretical results.
First Order Methods with Markovian Noise: from Acceleration to Variational Inequalities by Aleksandr Beznosikov, Sergey Samsonov, Marina Sheshukova, Alexander Gasnikov, Alexey Naumov, Eric Moulines
Stochastic optimization methods are key in machine learning. In theoretical studies of these methods, it is usually assumed that the randomness at each iteration is independent and unbiased. Meanwhile, there are many applications where such an assumption cannot be made and the situation is more complex. This paper delves into stochastic optimization problems that involve Markovian noise. We present a unified approach for the theoretical analysis of first-order gradient methods for stochastic optimization and variational inequalities. Our approach covers scenarios for both non-convex and strongly convex minimization problems. To achieve an optimal (linear) dependence on the mixing time of the underlying noise sequence, we use the randomized batching scheme, which is based on the multilevel Monte Carlo method. Moreover, our technique eliminates the limiting assumptions of previous research on Markov noise, such as the need for a bounded domain and uniformly bounded stochastic gradients. Our extension to variational inequalities under Markovian noise is original. Additionally, we provide lower bounds that match the oracle complexity of our method in the case of strongly convex optimization problems.