Papers accepted to ICLR 2024
Four papers by the Yandex Research team (shown in bold below) and our collaborators have been accepted for publication at the International Conference on Learning Representations (ICLR 2024).
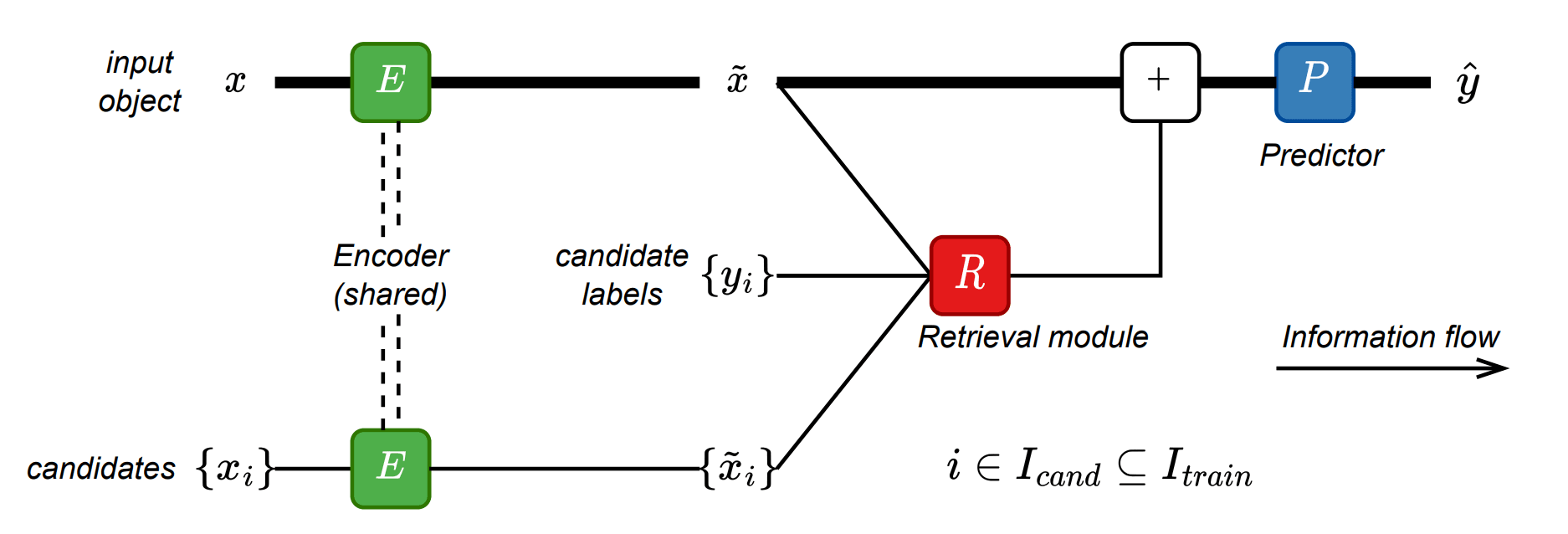
TabR: Tabular Deep Learning Meets Nearest Neighbors in 2023 by Yury Gorishniy, Ivan Rubachev, Nikolay Kartashev, Daniil Shlenskii, Akim Kotelnikov, Artem Babenko

Machine learning tasks on tabular data (e.g. regression, classification) are ubiquitous in real applications. In this work, we present TabR — a new deep learning model for such tabular tasks. Intuitively, TabR is just a combination of a simple feed-forward network and the old-but-gold k-nearest neighbors algorithm. Formally, TabR is a “retrieval-augmented model”, which means that, given an input object, it retrieves (similar) objects from the training data, and utilizes their features and even labels to make a better prediction. On a set of public academic benchmarks, TabR demonstrated the best performance among tabular DL models and, in particular, outperformed gradient-boosted decision trees. Retrieval-augmented models, such as TabR, have their set of practical limitations, but our work demonstrates the overall strong potential of this approach.
SpQR: A Sparse-Quantized Representation for Near-Lossless LLM Weight Compression by Tim Dettmers, Ruslan Svirschevski, Vage Egiazarian, Denis Kuznedelev, Elias Frantar, Saleh Ashkboos, Alexander Borzunov, Torsten Hoefler, Dan Alistarh
TL;DR We peer into the weights of large language models in search for insights on how to make these models smaller.
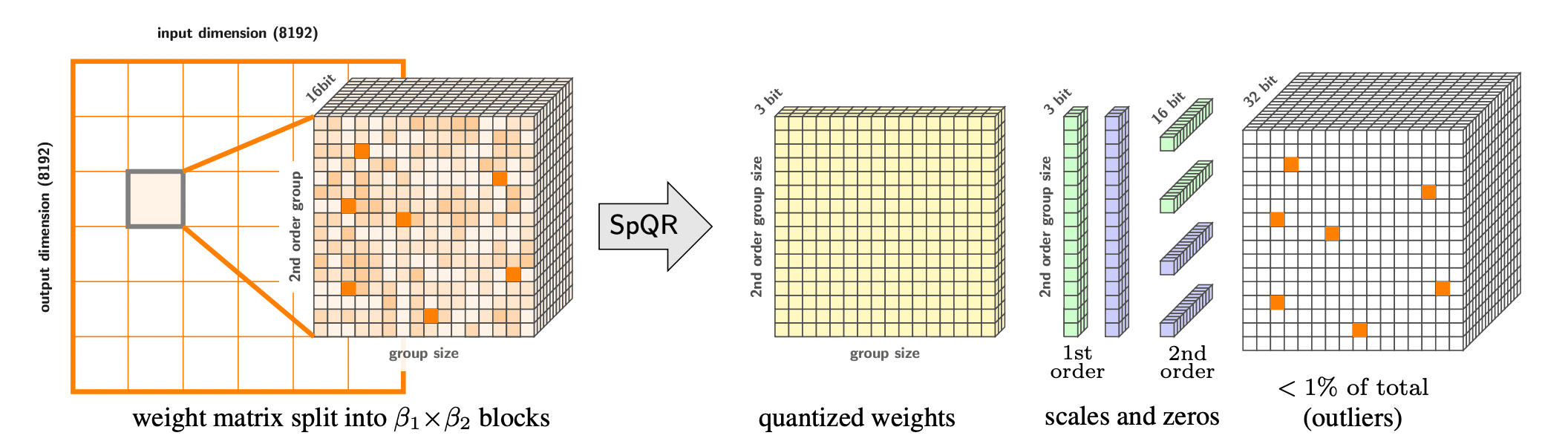
A high-level overview of the SpQR representation for a single weight tensor. The right side of the image depicts all stored data types and their dimensions.
Large language models (LLMs) can do awesome things, but they are, well… large. Running the best LLMs will cost you an arm, a leg, and a big expensive computer. If you want to run an LLM on a smaller computer, like your laptop, you need to compress them, e.g. by quantizing each weight to 4 bits. The problem is, if you quantize modern LLMs to less than 4 bits, they break down, so you can’t fit them into even smaller devices. In this paper, we explore how exactly they break down and find that there are a few (less than 1%) weights that can’t be quantized. We design an algorithm that finds these important weights and keeps them in higher precision, while quantizing the rest of the weights. This algorithm needs marginally more memory for the few important weights, but it quantizes the models much more accurately, outperforming all other known quantization algorithms.
Ito Diffusion Approximation of Universal Ito Chains for Sampling, Optimization and Boosting by Aleksei Ustimenko, Aleksandr Beznosikov
This work considers a rather general and broad class of Markov chains, Ito chains that look like Euler-Maryama discretization of some Stochastic Differential Equations. The chain we study is a unified framework for theoretical analysis. It comes with almost arbitrary isotropic and state-dependent noise instead of normal and state-independent one, as in most related papers. Moreover, our chain’s drift and diffusion coefficient can be inexact to cover a wide range of applications such as Stochastic Gradient Langevin Dynamics, sampling, Stochastic Gradient Descent, or Stochastic Gradient Boosting. We prove an upper bound for the Wasserstein-distance between laws of the Ito chain and the corresponding Stochastic Differential Equation. These results improve or cover most of the known estimates. Moreover, for some particular cases, our analysis is the first.
Neural Optimal Transport with General Cost Functionals by Arip Asadulaev, Alexander Korotin, Vage Egiazarian, Petr Mokrov, Evgeny Burnaev
In this research, we present a novel neural network algorithm for computing optimal transport (OT) plans for general cost functionals. Unlike common Euclidean costs, such functionals allow one to accommodate auxiliary information like class labels and pairs, providing flexibility. It extends to high-dimensional spaces, offering continuous OT solutions that generalize to new data points. Our work includes a theoretical error analysis and practical application to mapping data distributions while preserving class-wise structure.