
How to validate validation measures
In every practical machine learning task, there is a problem with measuring results. For deployed algorithms, we could consider real-life consequences like user growth or financial gain, but we need simpler performance measures during development. Meanwhile, different measures can lead to different evaluation results and, therefore, to different chosen algorithms. That is why it is essential to find an appropriate quality measure.
From classification and clustering to machine translation and segmentation tasks, many research fields have spawned their own well-established sets of traditionally used measures. Over the years, several attempts to compare performance measures were made, but the problem still lacks a systematic approach.
Performance measures and their inconsistency The link has been copied to clipboard
Classification is a typical machine learning task implemented in countless applications. Researchers usually compare the predicted labeling with the actual one to evaluate classification results using performance measures like accuracy, F-measure, etc. However, different measures behave differently. Below we show the inconsistency of some measures for the precipitation prediction task (see details in [2]). For this problem, the disagreement is enormous. Hence, it may significantly affect the decisions made.

| Accuracy | Balanced accuracy | Cohen's Kappa | F-measure | MCC | |
|---|---|---|---|---|---|
| Accuracy | — | 96.5% | 37.5% | 41.0% | 44.3% |
| Balanced accuracy | — | 58.9% | 55.6% | 52.0% | |
| Cohen's Kappa | — | 3.3% | 6.7% | ||
| F-measure | — | 3.4% | |||
| MCC | — |
Clustering is another widely used task that is helpful across various applications, including text mining, online advertisement, anomaly detection, and many others. The goal is to group similar objects. Here, the problem with quality measures is even more apparent: we have to compare the predicted partition with the actual one, which is non-trivial. For instance, can you guess which partition of objects better agrees with the actual one expressed by shapes and colors?
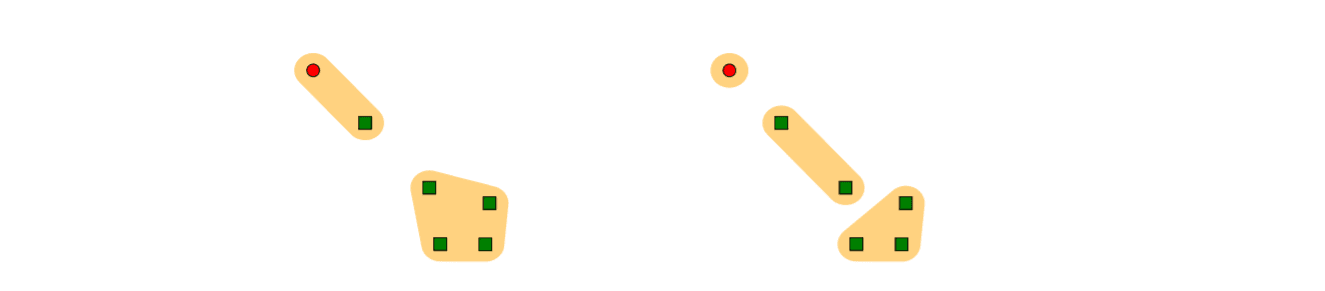
If you struggle to decide which one is better, no need to worry: known cluster similarity measures disagree on this simple example. For instance, widely used Rand, Adjusted Rand, and Jaccard measures prefer the left partition, while Variation of Information and Normalized Mutual Information prefer the right one. There are many other cluster similarity measures, and choosing the right one is debatable.
How to choose the right measure The link has been copied to clipboard
Therefore, we come to the question: how to choose a suitable measure? To answer it, we take a theoretical approach. First, we define some properties that are desirable for performance measures. For instance, one would expect a measure to attain its maximum value for a perfect prediction, while imperfect predictions are expected to have lower scores.
Constant baseline is a significant property. It requires a measure to lack bias towards particular class sizes (for classification) or cluster sizes (for clustering). Such preferences may lead to worse algorithms being unintentionally chosen for deployment. It turns out that almost all frequently used measures are subject to biases, both for classification and clustering tasks.
After formulating the properties, we formally check each for multiple known measures. Importantly, our research does not suggest ‘the perfect measure’ that should be chosen for all applications. Instead, we give a tool that helps to reject some unsuitable measures when specific properties are required for a particular application. Below is an example of what we get for some binary classification measures (including proposed ones).

Additional findings The link has been copied to clipboard
Our formal approach leads to further exciting insights. For instance, we noticed that no performance measure satisfies all the properties simultaneously. In particular, there are no measures that have the constant baseline property and can also be linearly transformed to a metric distance. It turns out that this is theoretically impossible, which means that at least one of these two properties has to be discarded.
If we relax the constant baseline property but require it to hold asymptotically, we have a measure satisfying all the remaining properties. This Correlation Distance can be used for both classification and clustering evaluation.
If we discard the distance requirement, the remaining properties can also be simultaneously satisfied. Symmetric Balanced Accuracy is one fascinating measure — the average between standard balanced accuracy and its symmetric counterpart. This measure has not been previously used for classification evaluation, and its analog was rarely used for clustering evaluation. Interestingly, good properties of Symmetric Balanced Accuracy are also preserved for the multiclass classification. It's the only measure that has this advantage.
We hope our work will prompt further research of performance measures for other more complicated tasks.
References
- Martijn Gösgens, Alexey Tikhonov and Liudmila Prokhorenkova. “Systematic Analysis of Cluster Similarity Indices: How to Validate Validation Measures.” ICML 2021.←
- Martijn Gösgens, Anton Zhiyanov, Alexey Tikhonov and Liudmila Prokhorenkova. “Good Classification Measures and How to Find Them.” NeurIPS 2021.←