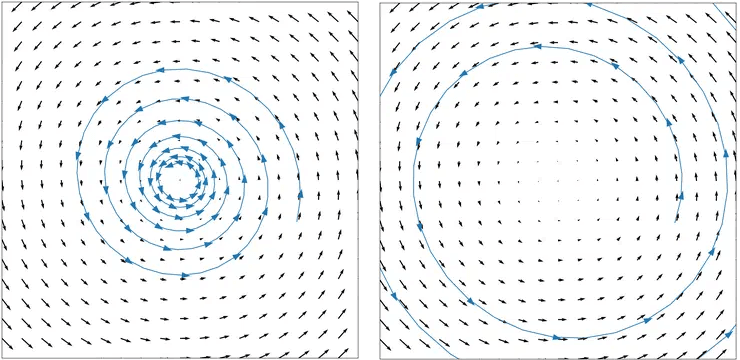
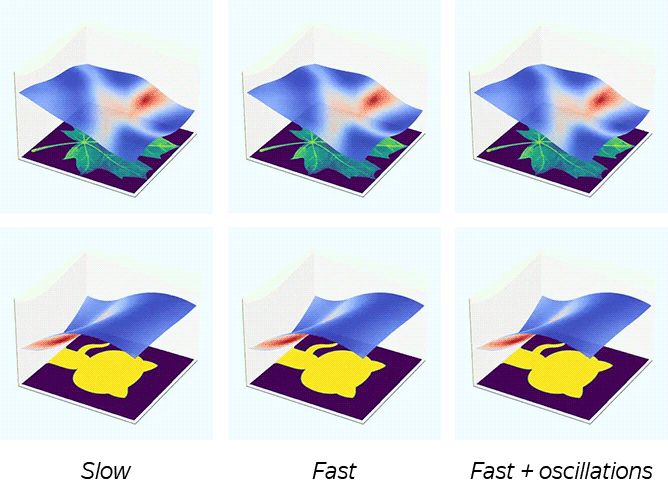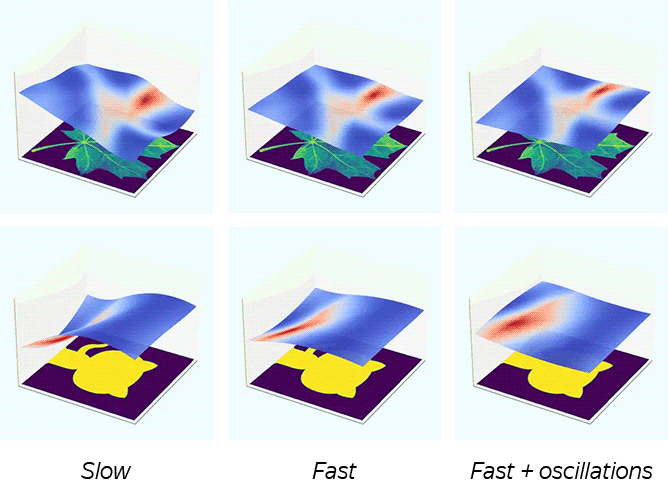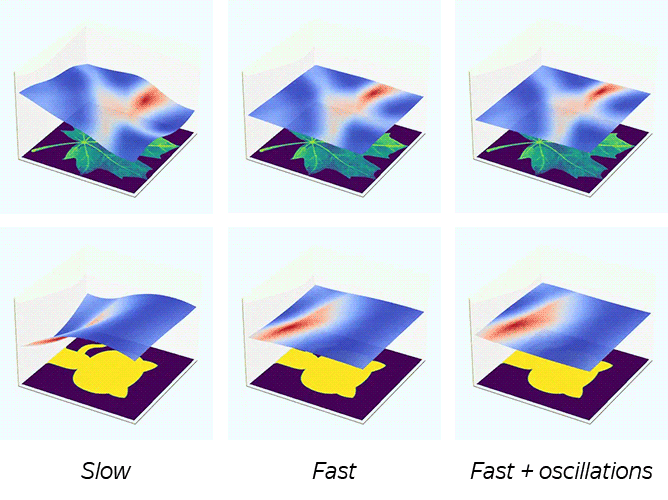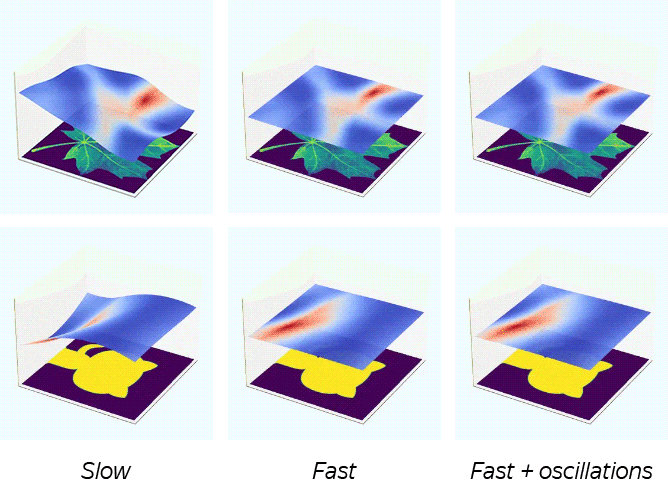
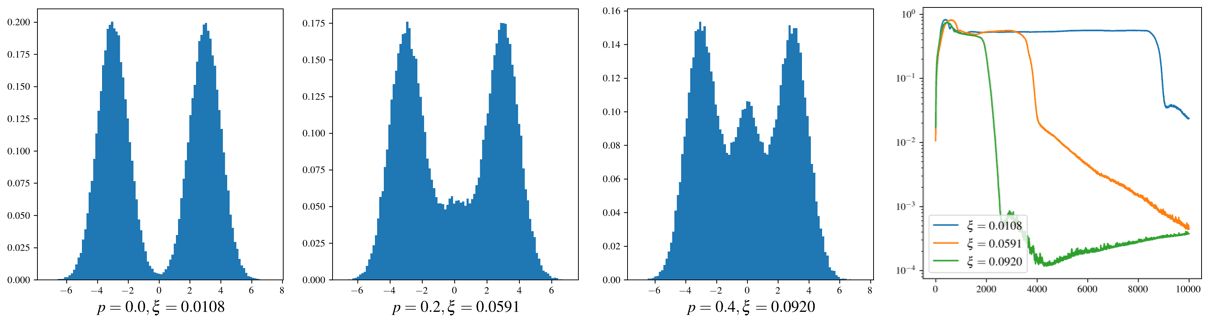
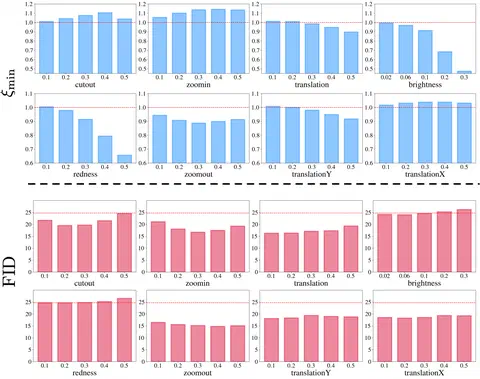
Figure taken from Training Generative Adversarial Networks by Solving Ordinary Differential Equations
Functional Space Analysis of Local GAN Convergence
Recent work demonstrated the benefits of studying continuous-time dynamics governing the GAN training. However, this dynamics is analyzed in the model parameter space, which results in finite-dimensional dynamical systems. We propose a novel perspective where we study the local dynamics of adversarial training in the general functional space and show how it can be represented as a system of partial differential equations. Thus, the convergence properties can be inferred from the eigenvalues of the resulting differential operator. We show that these eigenvalues can be efficiently estimated from the target dataset before training. Our perspective reveals several insights on the practical tricks commonly used to stabilize GANs, such as gradient penalty, data augmentation, and advanced integration schemes. As an immediate practical benefit, we demonstrate how one can a priori select an optimal data augmentation strategy for a particular generation task.
The convergence of GANs is known to be oscillatory and unstable. Many works analyzed their convergence in the parameter space from the point of view of a finite-dimensional ODE. However, the obtained theoretical results ignore the properties of the underlying measure. In practice, it is well-known that for certain datasets training GAN is much easier than for others. We show how the theoretical analysis in the functional space bridges convergence properties of a GAN and certain fundamental yet intuitive properties of the target dataset.
For instance, for the standard normal distribution the eigenfunctions can be computed analytically and are given by Hermite polynomials.
What determines the convergence? It turns out that the answer is given in terms of vibrational modes of the dataset! Formally, these numbers are eigenvalues of the Laplacian operator, associated with the given measure.
And the corresponding eigenvalue problem has the form:
We show that convergence is governed by the smallest non-zero eigenvalue also known as the Poincaré constant.
Small values correspond to disconnected datasets and deteriorate convergence speed. Higher values correspond to well-connected measures and improve convergence.
We visualize sample 2D distributions and various possible convergence regimes. For a fixed dataset, we obtain different behavior depending on the loss function used.
We can control the Poincaré constant by altering the dataset, for instance, by data augmentation.
A carefully constructed data augmentation improves the connectivity of a dataset, thus improving the convergence.
We show that this correlation exists for practical datasets such as CIFAR-10. Namely, we consider several possible common data augmentations, both spatial and color-based. As predicted by theory, we observe a negative correlation between the Poincaré constant of the (augmented) dataset and the FID score of a GAN trained with this specific data augmentation. Specifically, larger values of the Poincaré constant imply better connectivity and, thus, better GAN quality, resulting in lower FID.
In principle, this could allow us to discover optimal data augmentation protocols beforehand, since evaluating the Poincaré constant is much faster than training a generative model.
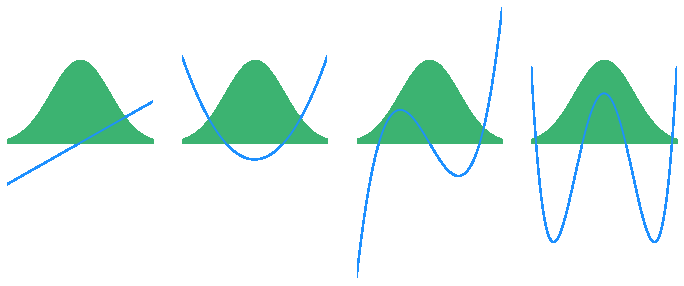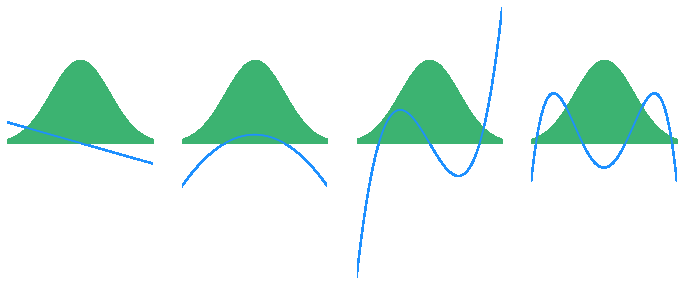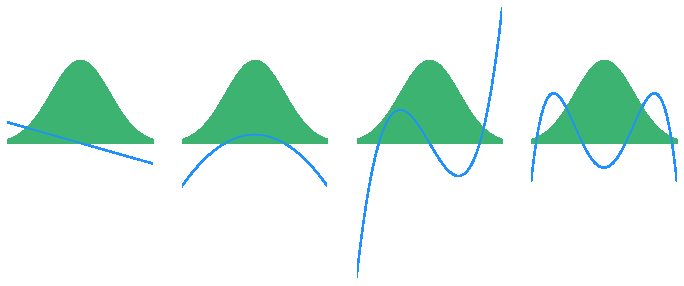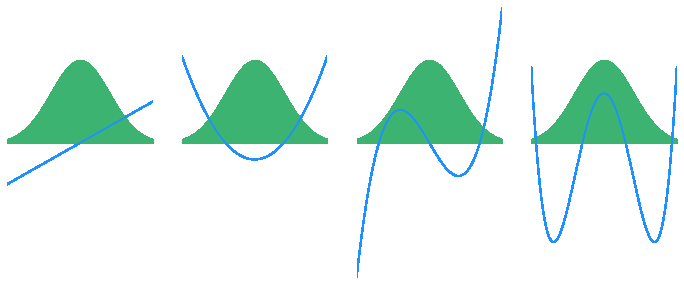
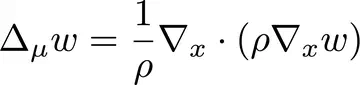
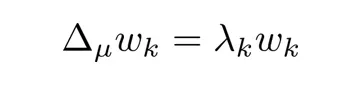
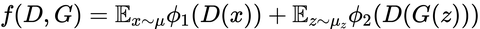
@inproceedings{khrulkov2021functional,
title={Functional Space Analysis of Local GAN Convergence},
author={Khrulkov, Valentin and Babenko, Artem and Oseledets, Ivan},
booktitle={International Conference on Machine Learning},
year={2021}, organization={PMLR}
}