Embeddings for numerical features in tabular deep learning

Tabular data appears in many production systems. Recommender algorithms, delivery time estimation, fraud detection and other applications rely on processing tabular data. At Yandex Research, we actively contribute to the field of tabular machine learning.

In this post, we share exciting findings from our recent NeurIPS 2022 paper on deep learning and tabular data

[1]. We discuss how improved representations of numerical features can turn your vanilla MLPs (multilayer perceptrons) and Transformers into state-of-the-art tabular deep learning solutions that are competitive even with gradient-boosted decision trees, one of the strongest baselines in the world of tabular data problems!

The ubiquitous transformers The link has been copied to clipboard

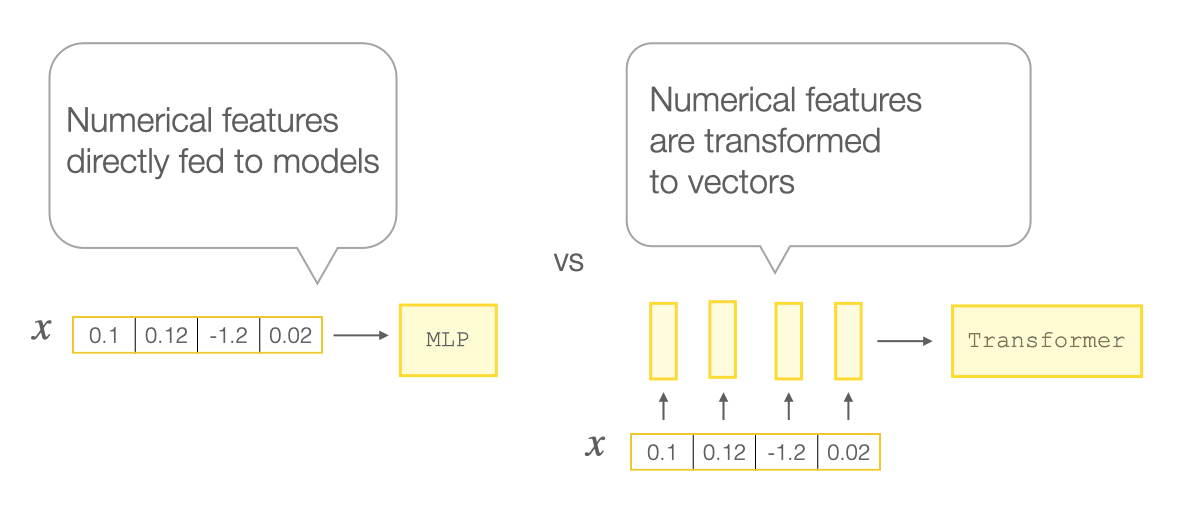
With Transformers taking over deep learning by storm, tabular data was no exception. Multiple works proposed Transformer-based architectures for tabular data, which outperformed MLP-like models

[2]

[3]. Compared to MLPs, the proposed Transformer architectures handle numerical features in a special way: they map scalar values of numerical features to high-dimensional embedding vectors, as shown in the picture below. Typically, this mapping is simple (e.g. a linear layer) and is not considered an important design choice. However, as we will see below, this mapping can significantly impact performance!

The crucial insights on the importance of input representation The link has been copied to clipboard

Apart from the above note on the transformers, we had one more important source of inspiration. In fact, proper input handling is one of the central topics in the field of implicit neural representations. In this field, neural networks are trained to map coordinate-like inputs (which are numerical features!) to different forms of content.

For example, the figure below illustrates how a neural network can fit an RGB image, which is equivalent to solving three tabular regression problems. In this specific example, the authors of

[4] demonstrated that a special input representation based on the Fourier Features allows solving the problem with dramatically better results compared to the raw scalar coordinates.

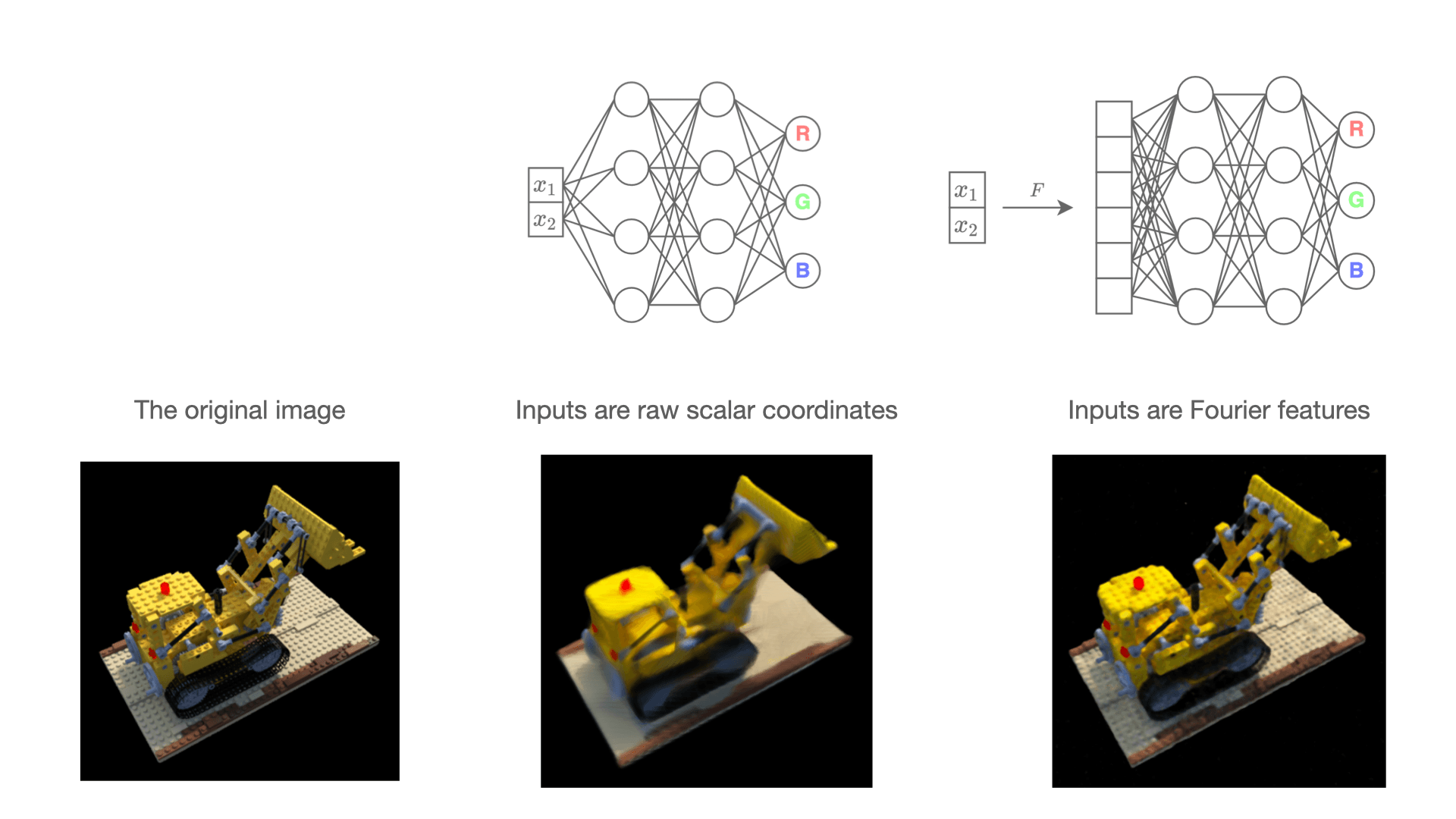
In fact, the above example showcases the fundamental limitations of training MLPs with gradient-based optimization. However, this is a whole different story. To learn more, we recommend the original paper [4] as a great entry point to the topic.

Overall, after making the above observations on the Transformers and implicit neural representations, we decided to explore different ways of encoding the numerical features before passing them to neural network backbones.

Piecewise linear encodings The link has been copied to clipboard

We start with “classical” machine learning techniques. We take inspiration from the one-hot encoding and adapt it for numerical features. Namely, for a given feature, we split its value range into bins and build the encoding as shown in the figure below (the example illustrates the encoding with four bins):

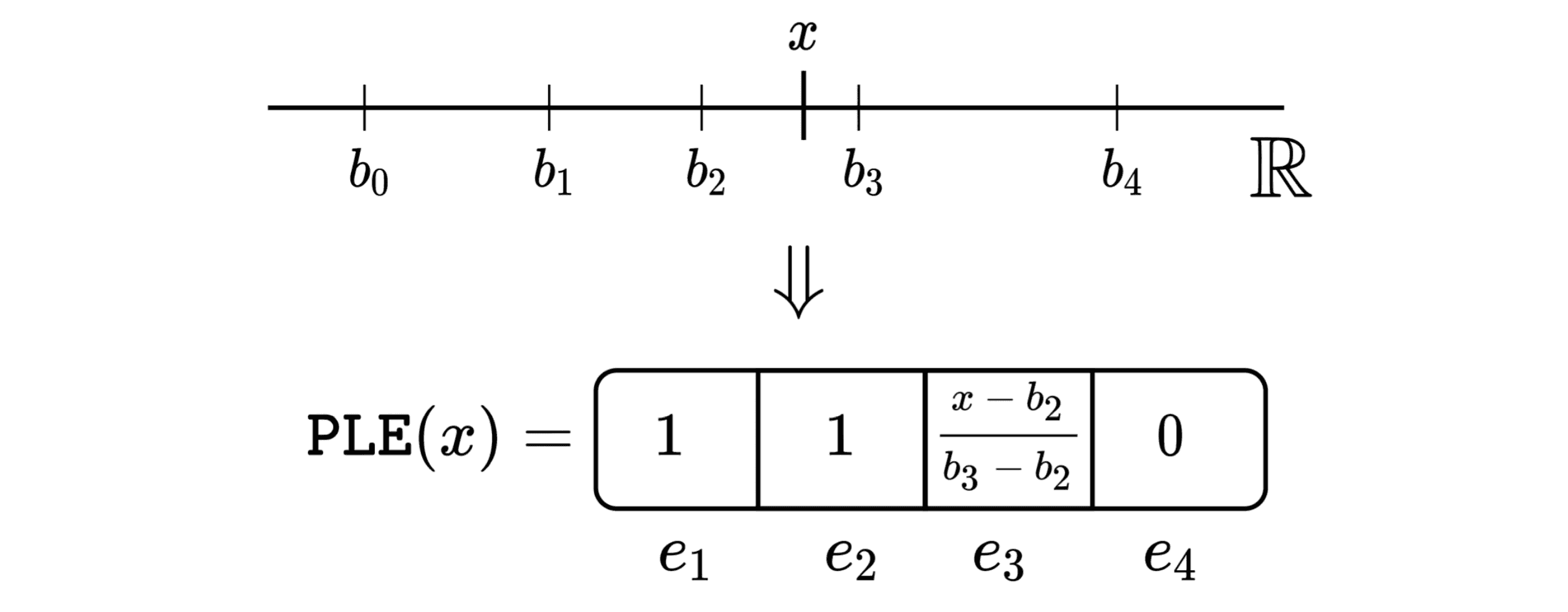
In the paper, we describe two ways of obtaining the bins and compare the scheme with the well-known feature binning technique.

Encoding with periodic activation functions The link has been copied to clipboard

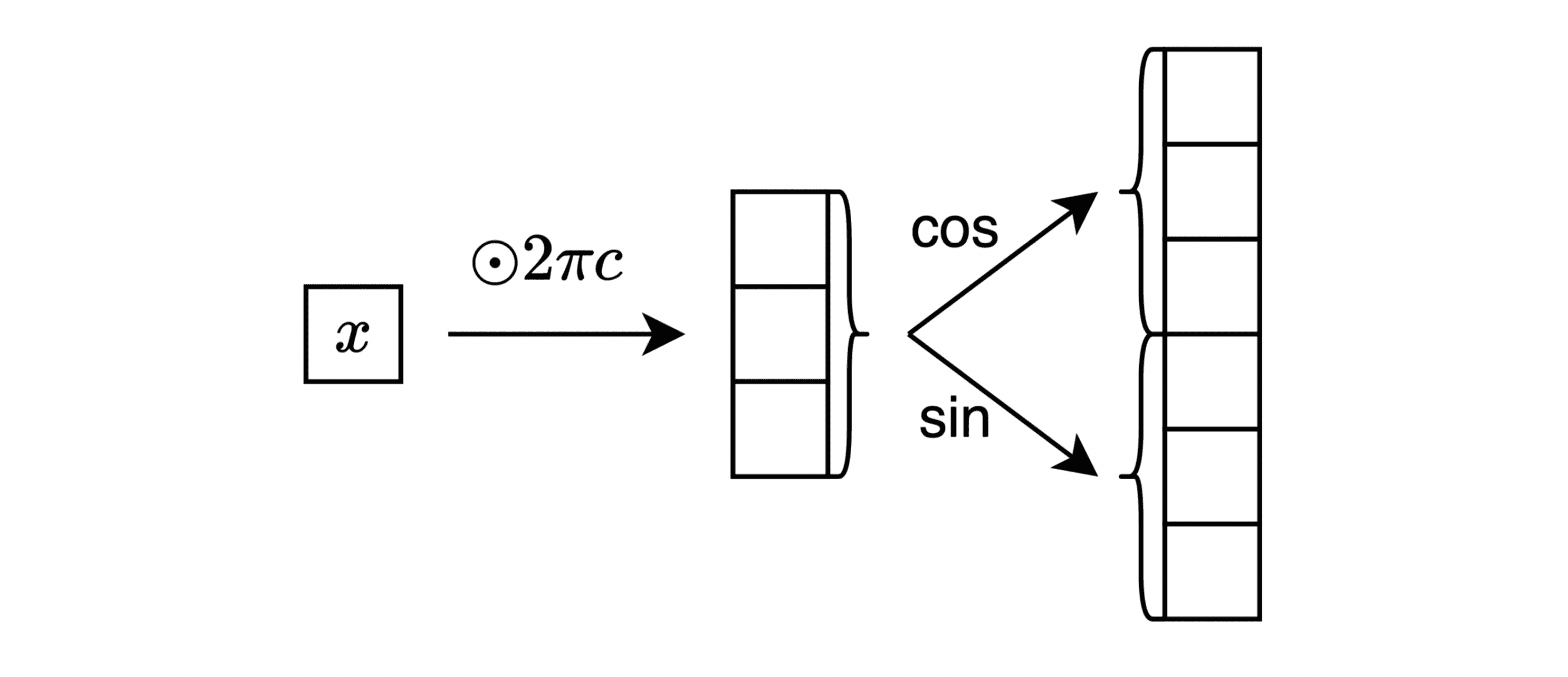
The second numerical embedding scheme is inspired by the success of periodic activations in the implicit neural representations. The specific embedding module is illustrated in the figure below. Importantly, we empirically observed that the initialization scale of the vector of “frequencies” (denoted as “c” in the figure) has a significant impact on the final performance.

Using numerical feature embeddings The link has been copied to clipboard

While embedding modules described above enabled us to achieve good results, we observed that adding a linear layer with the ReLU non-linearity on top of them usually improves the results even further.

We apply the embeddings to both MLPs and Transformers. We pass embeddings to Transformers in a usual manner as a set of vectors. When passing embeddings to MLP, we simply concatenate them as shown below:

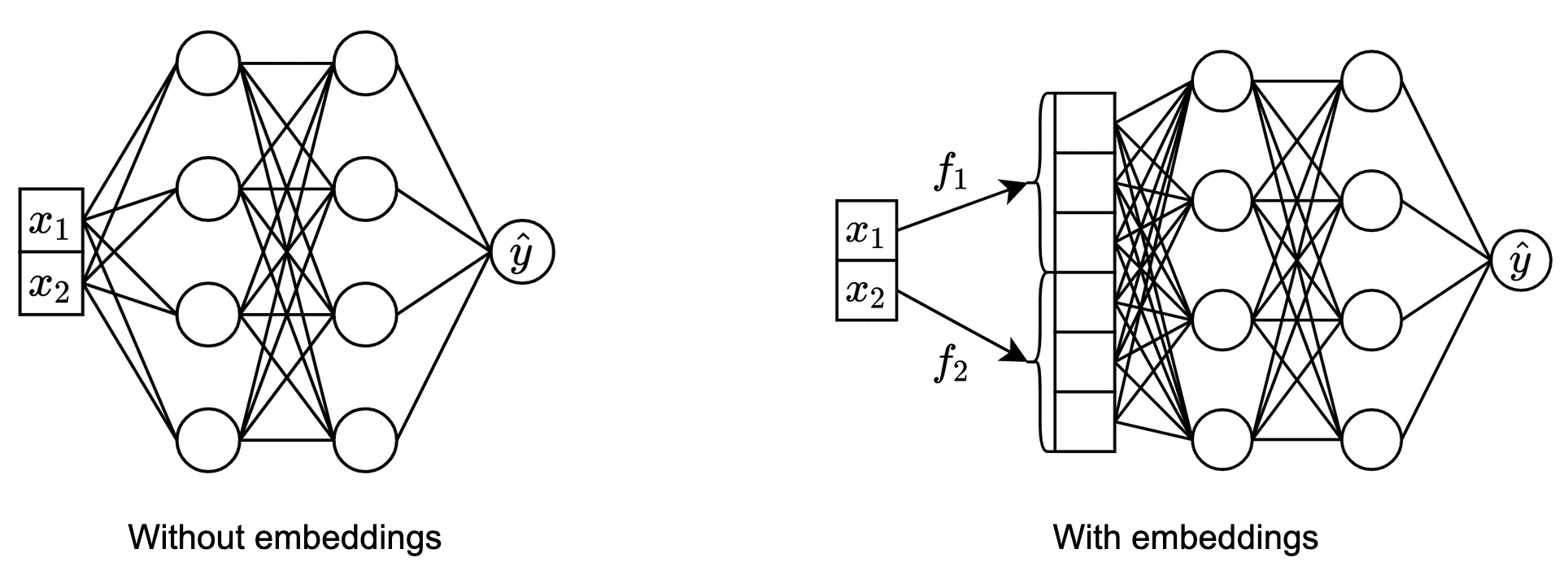
Results The link has been copied to clipboard

The results are inspiring, to say the least! On a tabular benchmark, where baseline neural networks lag behind well-tuned gradient-boosted decision trees, the addition of embeddings to numerical features makes neural networks competitive with the tree-based models!

The second significant result is that MLP equipped with embeddings for numerical features performs on par with the heavy Transformer architecture.

Backbone	Embedding	Average rank (std. dev.)
XGBoost	–	4.6 (2.7)
CatBoost	–	3.6 (2.9)
MLP	–	8.5 (2.6)
Transformer	Linear	5.9 (2.2)
MLP	PLE + Linear + ReLU	5.1 (1.7)
MLP	Periodic + Linear + ReLU	3.0 (2.4)
Transformer	PLE + Linear + ReLU	3.7 (2.2)
Transformer	Periodic + Linear + ReLU	3.9 (2.5)

Summary The link has been copied to clipboard

We found that embeddings for numerical features can provide significant performance improvements for tabular deep models, and make vanilla MLPs competitive with heavy Transformer models.

That said, we only scratched the surface here. We certainly did not cover all possible embeddings, and choosing the best hyperparameters may still be an issue. Nevertheless, we are excited to share these results and continue to work on understanding and building upon them.

The source code for reproducing our experiments is available on GitHub.